因数 分解 公式 3 乗 128918-��数分解 公式 3乗

 因数分解の公式②：2乗公式と3乗公式 続いて2乗公式と3乗公式です。 公式としては以下の通りになります。 1 a22abb2= (ab)2 2 a22abb2= (ab)2 3 a33a2b3ab2b3= (ab)3 4 a33a2b3ab2b3= (ab)3 見破るポイントとしては、1番初めの数字と1番後の数字が2乗の形か3乗の形になっている場合ですね。 3乗公式は間に数字が2つ出てくる場合が多いので、見です。因数分解をたすきがけで解く方法は、他の問題にも適用できます。 因数分解の問題 下記の整式を因数分解してください。 1問目は、3乗の因数分解の公式を思い出してください。 のとき、a=2a 、b=1ですね。よって、因数分解すると です。因数分解の解法マニュアル どんな問題もまずⅠ，Ⅱ，Ⅲを試みます． Ⅰ 共通因数があればくくる(全体ではなく個別にくくっても可) Ⅱ 因数分解の公式が使えるか検討する(上の公式⑥はたすきがけで対処)． Ⅲ 同じ形を別の文字で置き換える．その後，因数分解の公式が使える形まで変形．

高校数学 数 第1章 数と式 12 文字が3種類ある3乗の公式 壱のblog

因数分解 公式 3乗

因数分解 公式 3乗- 例：x² – 9を因数分解する 定数項9は3の2乗。 よって解答はx² – 9 = (x – 3) (x 3)となります。 よく使う数字の2乗 因数分解でよく使われる2乗を覚えておくと便利です！ いちいち筆算する必要がなくなり、テストでも時間の節約になります。 3 乗の和・3 乗の差の因数分解 公式 どちらの公式にもプラス・マイナスの双方が登場するので、覚え間違いに注意しましょう。

高校数学 3乗の展開 因数分解公式の覚え方 その2 By 家ゼミ Youtube

 これが分解前の体積 $(xy)^3$ と同じになります。これはまさしく、 3乗の展開・因数分解の公式そのもの ですね。 こうして、3乗の展開・因数分解の公式は、立方体の分割で考えることができることがわかりました。 定数項が \(−4\) のため、何かの \(3\) 乗とは考えにくく、因数分解の公式には当てはまらなそうです。 このような場合に因数定理を利用して最初の因数を探します。 適当な値を \(x\) に代入してもいいですし、因数の見つけ方のコツを使ってもよいです。 x 3 – y 3 = (x – y) (x 2 xy y 2) のように因数分解できることがわかります。 同じように、(x y) 3 を計算することで、x 3 y 3 も因数分解できますので、レッツトライ。 記憶すべき変形

 a^3b^3c^33abc\\ = (abc) (a^2b^2c^2abbcca) a3 b3 c3 −3abc = (a b c)(a2 b2 c2 −ab− bc −ca) 教科書レベルを少し越えていますが，難関大を受験する人たちはみんな覚えている有名な因数分解公式です。 「3つの3乗」が出てきたら，この公式を思い出しましょう。 特に c c c が具体的な数字のときには左辺の形に気づきにくい ので注意しましょう。 例 c = 13次式以上の因数分解練習問題 利用するのは主に\(\,3\,\)次式の因数分解公式です。 \(①\hspace{4pt}\color{red}{a^3b^3=(ab)(a^2abb^2)}\) \(②\hspace{4pt}\color{red}{a^33a^2b3ab^2b^3=(ab)^3}\) 上の公式で\(\,b\,\)の代わり 因数分解公式3 因数分解 因数分解公式のなかでもわりと理解しやすく、簡単に感じるかもしれません。 この2乗引く2乗の形は今後さまざまな分野で使われるため応用が利くことで特に重要なものです。 2乗の元 (平方根)がすぐに出てくるように

 の項を足したり引いたりして、式のつじつまを合わせる 。 (3) これも発想としては (2)と同じ。 を の形にするため に を補うと、 前側 と 後ろ側 を分けて 因数分解 すると、「2乗－2乗」の形になる。 ・・・答 ※ を 因数分解 せよ 例えばしたの例では\((a3)\)が共通因数になります。 例 共通因数でくくる因数分解 最低次数で整理する 「公式に当てはめられない」、「共通因数も見つからない」という場合は、「最低次数で整理する」ということを試してみると解けることがあります。 考え方は単純で、3乗の因数分解が無理なら2乗の因数分解へと変化させよう（次数を下げよう）と考えればよいのです。 その方法は、とにかく勘に従って1つ数字を入れてみるというものです。 例えば、上記の②の3乗多項式にx=1を代入してみます。 するとどうなるか。 左辺の値は=0となり、右辺と一致します。 という事は左辺の3乗の方程式は因数分解する

1

高校数学 数 第1章 数と式 12 文字が3種類ある3乗の公式 壱のblog

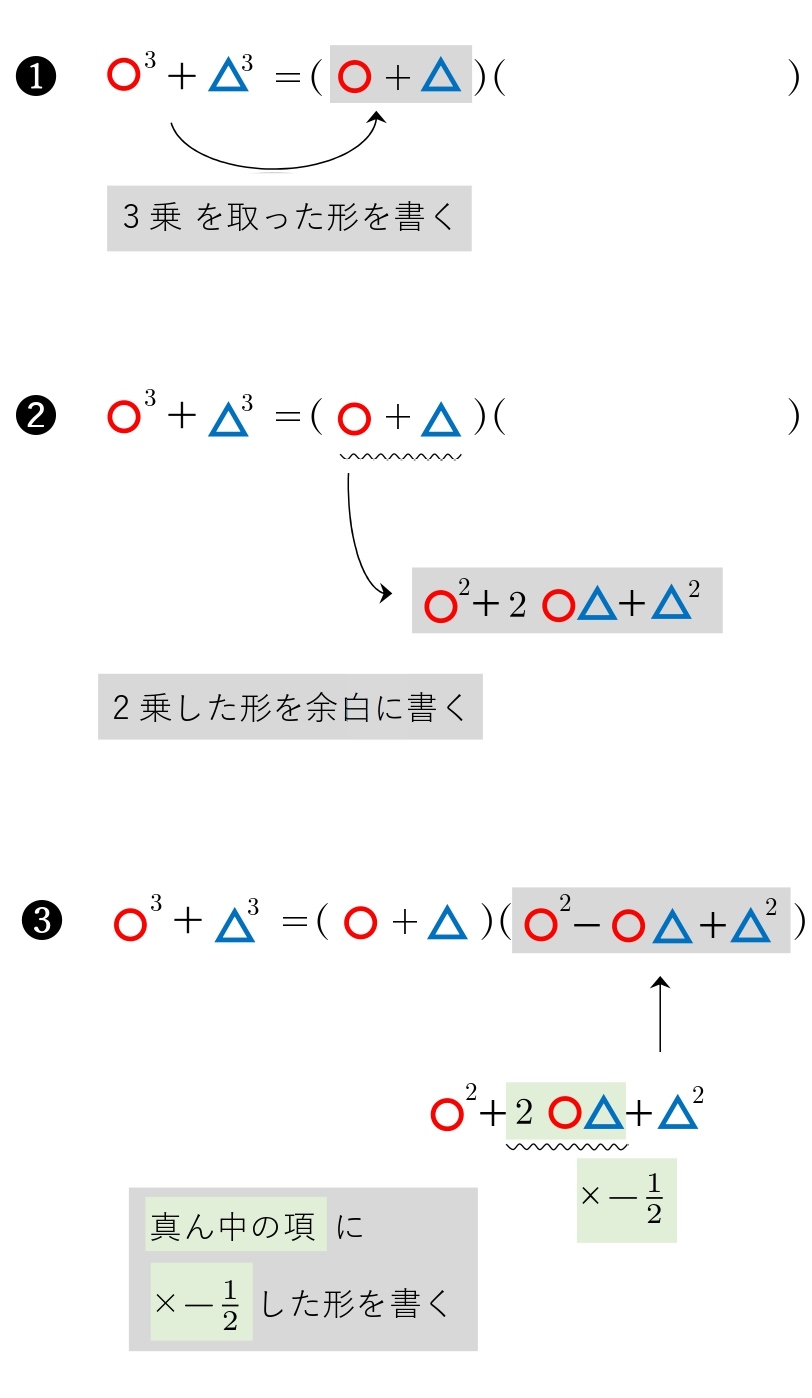
 確認まずは、後で使う2次と3次の因数分解の公式を確認しておきましょう。2次の因数分解の公式平方の差の因数分解公式： 3次の因数分解の公式立方の和と差の因数分解公式： 6次の因数分解さて、上記の公式を使って、6乗の差を因数分解してみましょう： この因数分解を2通りで行って 多項式の基本6｜3次以上の展開と因数分解の公式の総まとめ 前々回の記事で説明したように，たとえば x 2 − 2 x − 2 = 0 のような簡単には因数分解できない2次方程式は，いったん解を求めることによって因数分解できるのでした． では，3次式では因数分解一番使用頻度が高いのがこの公式です。 例題を見ながら公式の使い方を確認しておきましょう。 例題 次の式を因数分解せよ。 式を見たときに、 (三乗)＋ (三乗)、 (三乗)－ (三乗)の形 になっていれば、この公式を使うことができます。 ここでは、どんな数が3乗の形になるのかを判断できるようにしておく必要があります。 よく出てくる3乗の形は以下の通り

因数分解とは 公式と計算のやり方を覚えて問題を解いてみよう 中学 高校数学 テラコヤプラス By Ameba

平方完成 多項式の因数分解 優技録

今回のテーマは「3乗の因数分解公式」です。 a 3 ±b 3 はどのようなカタチに因数分解できるか、みなさんわかりますか？ ポイントをおさえればすぐに覚えられます。 さっそくa 3 ＋b 3 の因数分解公式を見てみましょう。 タイトルの画像にある因数分解の公式 僕は中学3年生のときに学びました。 a^2 − b^2 = (ab)(a−b) (^2 は「2乗」を表しています) 通称：2乗−2乗 (にじょうまいなすにじょう) ですね。皆さんは覚えていますか？ 数学が嫌いだった方は、 「どうしてこんな公式覚えなきゃいけないんだ 因数分解の公式を覚えない！ 因数分解の基本公式を覚えることが一番いい方法なのは間違いありません。 \begin{align} \text{① } & x^2 2xy y^2 = (xy)^2 \\ \text{② } & x^2 – 2xy y^2 = (xy)^2 \\ \text{③ } & x^2 – y^2 = (xy)(xy) \\ \text{④ } &

３次方程式まとめ 解き方 因数分解 解と係数の関係 理系ラボ

３次以上の展開と因数分解はどうなる 公式の総まとめ

因数分解のやり方・公式 3 パターン 1 、 x 2 から何かの 2 乗を引いた式に使う公式 ・ x 2 − a 2 = ( x a) ( x − a) 2 、 x の係数を半分にして 2 乗すると 定数項と同じになる式に使う公式 ・ x 2 2 a x a 2 = ( x a) 2 ・ x 2 − 2 a x a 2 = ( x − a) 2 3 、掛けると 因数分解2乗の公式 特に重要なのが、④の公式です。 ④の公式に \(a=y,b=y\) を代入すると①の公式になり、\(a=y,b=y\) を代入すると②の公式になり、\(a=y,b=y\) を代入すると③の公式因数分解のやり方・公式まとめ ・ \ (x\)の係数を半分にして、\ (2\)乗する ・ 求めた値と定数項が同じときは \ (x\)の係数を半分にした値で因数分解する 因数分解の公式半分の\ (2\)乗 ・ \ (x^22axa^2= (xa)^2\) ・ \ (x^22axa^2= (xa)^2\) 因数分解 やり方

3

3乗の因数分解 展開 公式 理系ラボ

 この変形後の式で、1つ目と3つ目に注目してみましょう。 「3乗足す3乗」の形になっていますね。 三次式の因数分解の式が使うと、 a b c a b c が出てきます。 また、2つ目と4つ目に注目すると、 3ab 3 a b でくくれば、こちらからも a b c a b c が出てきます。 なので、まとめられそうですね。 まとめると、次のように変形できます。 (a b)3 c3 −3ab(a b中学数学 因数分解 公式3 "2乗の差"因数分解はこれから先ずっと使ってゆきます。映像授業を駆使し塾に通えない生徒の皆さんにも授業配信 3乗の因数分解（展開）公式 理系ラボ 数学Ⅱ 3乗の因数分解（展開）公式 目次 非表示 1 3次式の因数分解・展開の公式まとめ 2 2次式の因数分解・展開の公式まとめ（復習） 3 3次式の因数分解の例 東大塾長の山田です。 このページでは、 「 3 次式の因数分解・展開の公式 」について解説します 。

３乗とは 1分でわかる意味 求め方 展開 因数分解 展開公式との関係

3

 2乗・3乗の公式 因数分解は、 「式の展開」の反対 に相当する変形です。 カッコの中を1つずつかけ算していけば求まる「展開」と異なり、因数分解は 公式を知らないと解き方の検討がつかない ケースもあります。 因数分解の公式（乗法公式） 中3で習う公式はこの3つ。 なぜこうなるのか、という説明として「 右辺を展開すればもとに戻る 」と教わることがほとんどだと思いますが、この公式の導出についてはあまり教わらないっぽいので、その導出方法を解説します。 教科書レベルを少し越えていますが，難関大を受験する人たちはみんな覚えている有名な因数分解公式です。 「3つの3乗」が出てきたら，この公式を思い出しましょう。 特に c c c が具体的な数字のときには左辺の形に気づきにくい ので注意しましょう。

数学 B 1の3乗根に関する問題 長崎大 九州歯科大 広島工業大 大学入試数学の考え方と解法

因数分解のやり方がわからない人必見 公式や解き方のコツをわかりやすく紹介 高校生向け受験応援メディア 受験のミカタ

16年10月5日 / 最終更新日 16年10月5日 matsu 数学Ⅰ 因数分解 3乗の公式 3乗の公式 パン太先生 今回は3乗の形の因数分解について学びましょう。さっそく公式 因数分解の公式はよく教科書にわかりやすく載っていますが、複素数をつかった因数分解の公式はあまり載っていません。 最も簡単な例は、\(\displaystyle a^2b^2\)の因数分解です。 3乗 今回は、中学3年の数学で学習する「因数分解」について、記事を書いていきたいと思います。 この記事では、 「そもそも因数分解ってなに？」 「展開と因数分解はどう違うの？」 「どの乗法公式で因数分解すればいいの？」 という中学生に、基本からわ

数と式 因数分解の公式 3乗の公式 その2 Vol 16 ３回読めば 絶対理解できる看護受験数学 Kazアカデミー 大阪の看護学校 看護予備校

高校数学 因数分解 解の公式を使ってルートが登場する因数分解を解けるようになろう 数学の面白いこと 役に立つことをまとめたサイト

多項式 例題 多項式と単項式の乗法除法 式の展開 乗法公式(xa)(xb)の展開 乗法公式 2乗の展開 乗法公式 和と差の積の展開 式の展開 いろいろな計算 式の展開 四則 因数分解1_共通因数をくくりだす 因数分解2_(xa)(xb) 因数分解3_2乗 因数分解4_(xa)(xa) 因数分解 おきかえ 共通因数をくくりだした後 この記事では、「因数分解」について、その公式や計算方法をできるだけわかりやすく解説していきます。 この記事を通して、ぜひ因数分解をマスターしてくださいね！ 目次因数分解とは？因数分解の公式2 乗の公式3 乗の公式たす 3乗の差の因数分解公式を利用しよう。 8 a 3 − 125 b 3 = ( 2 a) 3 − ( 5 b) 3 = ( 2 a − 5 b) ( 4 a 2 10 a b 25 b 2) 54 x 3 − 16 y 3 (3)の考え方と解答 54と16は立方数ではないから，3乗の差にはなっていない。 しかし，因数分解で最も大切なことは共通因数でくくる

例題 ３乗の因数分解 Youtube

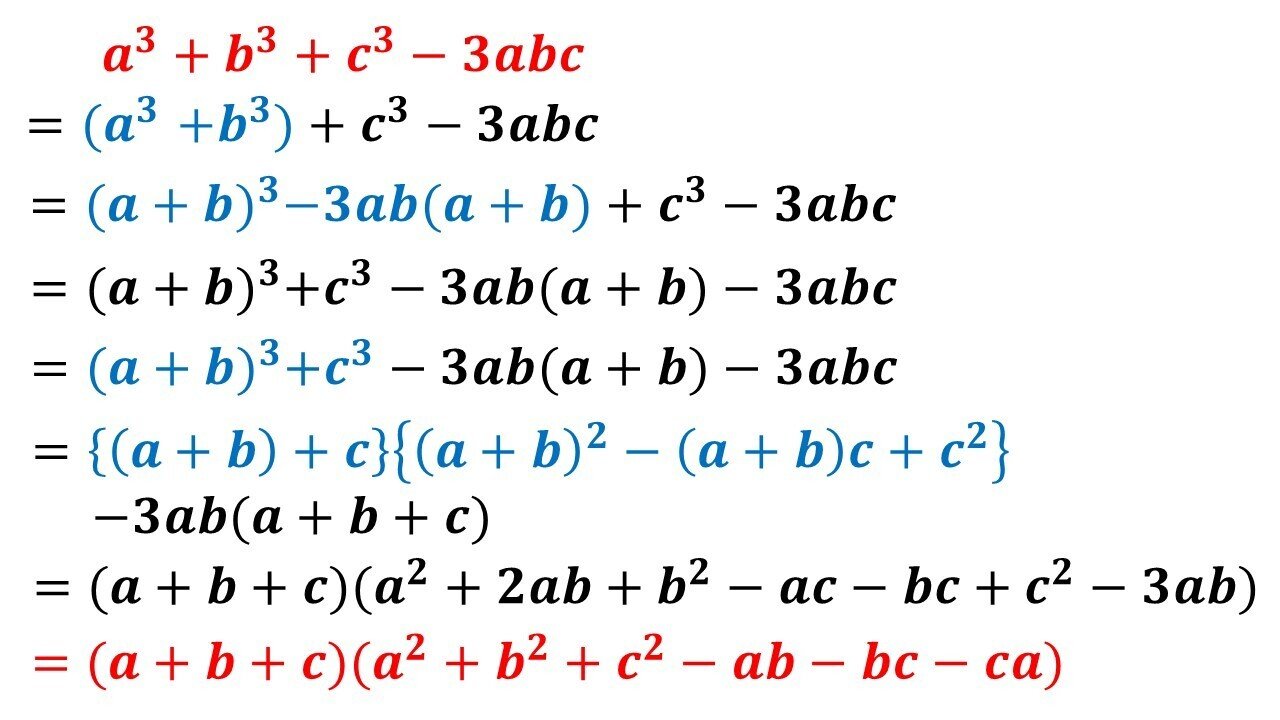
3乗の対称式だけど基本対称式を考えずに因数分解するもの タロウ岩井のnote Note

高校数学 3乗の展開 因数分解公式の覚え方 その1 By 家ゼミ Youtube

対称式の変形まとめ 基本公式を覚えてサクサク計算しよう 数スタ

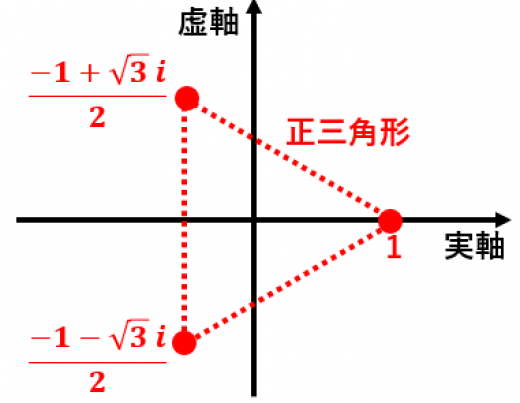
１の三乗根オメガを用いた計算と因数分解 高校数学の美しい物語

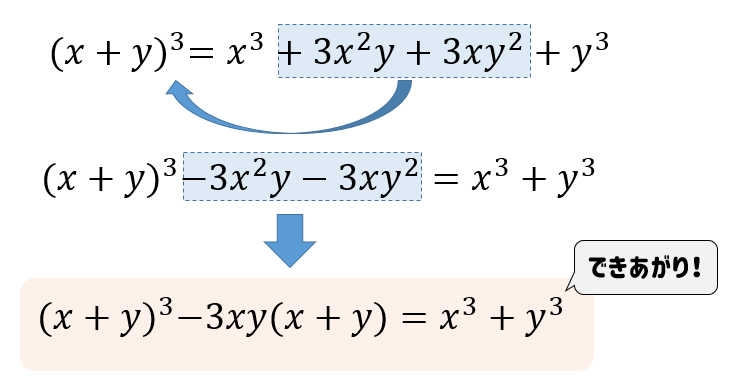
二乗足す二乗の公式 なんでこんな変形になる どんな場面で活用する 数スタ

3

一度は解いておきたい ３乗の因数分解の解説 鳩の家庭教師in川口市 参考書学習をサポートします

新高1 数学 ａ ４ｓｔｅｐほか 上北沢 哲英会 個人塾 連絡用ブログ

高校数学 ３次式の展開 因数分解 公式 覚え方 計算方法 学校よりわかりやすいサイト

3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す

高校数学 数 10 因数分解 応用編 Youtube

中３ 式の計算 因数分解 公式編 設計図の選び方と使い方 あとはパズル 教えたい 人のための 数学講座

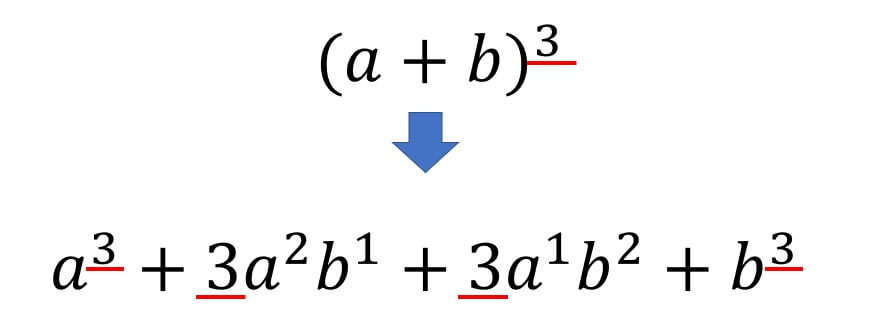
三乗の公式 A B 3乗の展開公式と覚え方を解説

2

展開と因数分解公式 大学受験の王道

数学 因数分解 3乗公式 数学

高校数学 因数分解公式と3次式の因数分解 受験の月

三乗公式 展開 因数分解 の覚え方 展開の楽な方法 Youtube

数学 ３次式の因数分解の公式の使い方とコツ ページ 2 教科書より詳しい高校数学

第4講 3次式の展開と因数分解 １章１節式の計算 問題集 高校数学

三乗の公式 展開と因数分解 高校生向け受験応援メディア 受験のミカタ

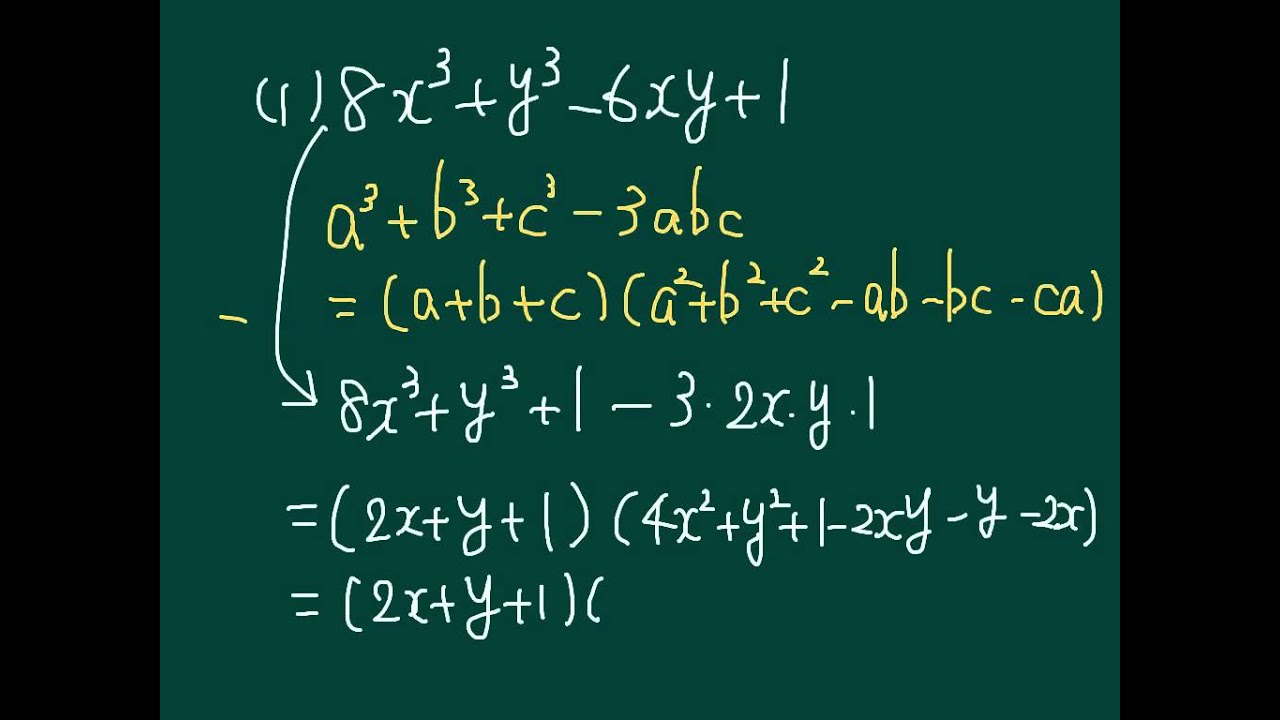
因数分解 三乗の公式の利用 Youtube

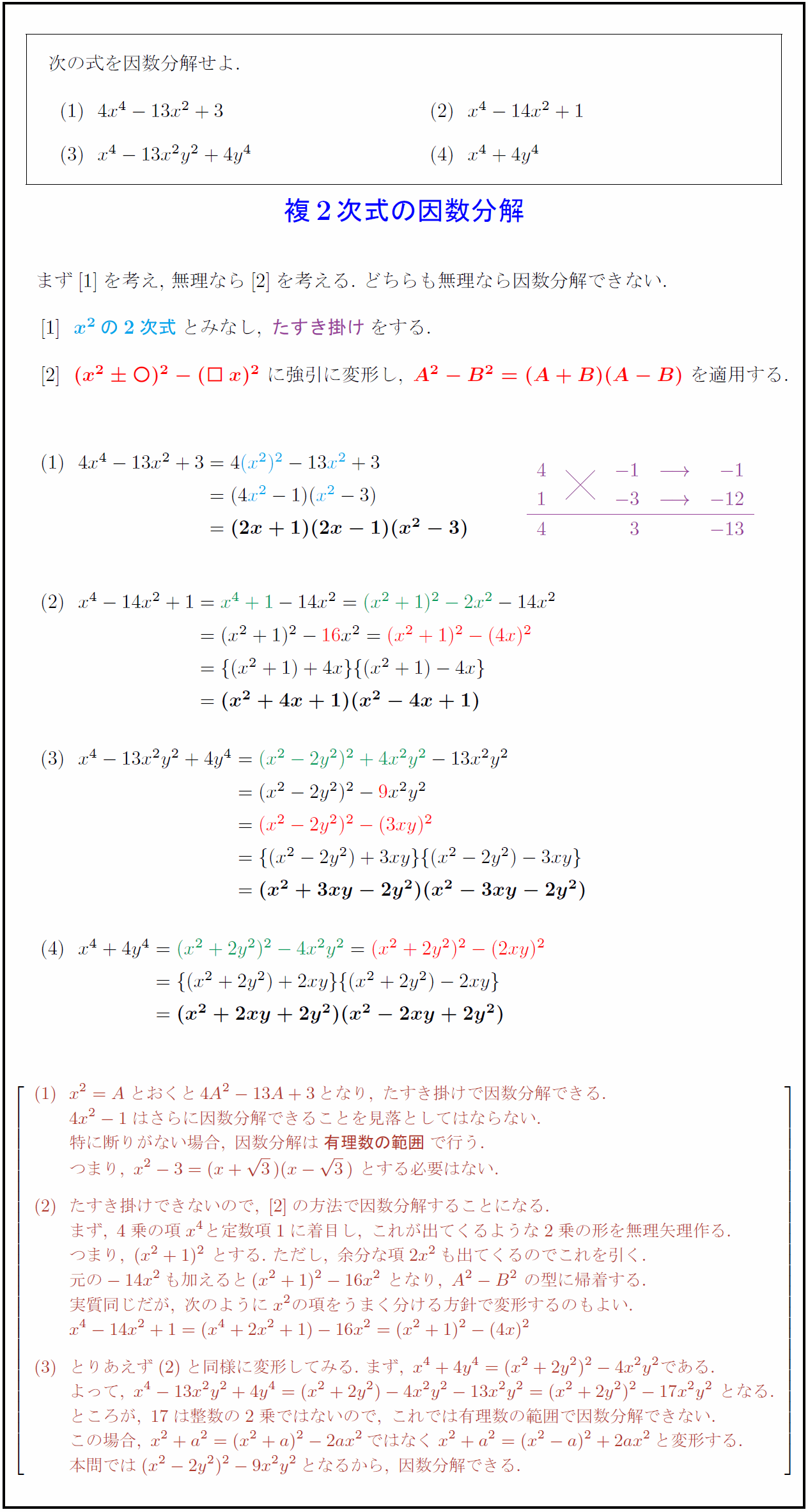
高校数学 複2次式 2乗の2次式ax Bx C の因数分解 受験の月

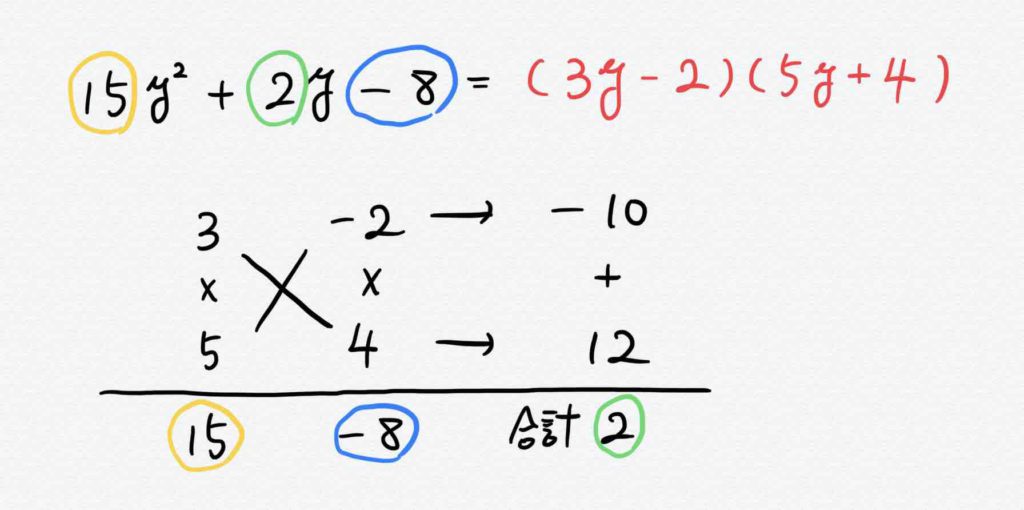
公式いろいろ 因数分解のいろいろな問題とその解き方 スタディクラブ情報局

高校数学 3乗の展開 因数分解公式の覚え方 その2 By 家ゼミ Youtube

A B 3 公式 三乗の公式 展開 A B 3はどうやってやる 中 Qhcoh

Lh3 Googleusercontent Com Proxy Zobijrxk384vn06h67 Freqc9gfz4gsedgtlgzfooctwyho1d56bjysajvmch30l3stvcv8npccizy 13mbswrxno1wrhguqw7eszoolt7tzg Tjah6mzshvrw3kjfqvcf41c Pkkyyazrzjmnzfmspygeqqte5h4g1expbphxhfp6lyqve Bhqoyznottz2flr M2w Rkn2b9tzs0dabzn2p2e7jtealxb4z 8zc6d0ca8c2rthkbr9oje0o7j Deeq3dvaejdh6clpef Bxp4kamiy1d1rdb6xn6ynr65qp4l9w Gv Ppypmydjo5rgj2mvsztrykq6acfrhvqmcoj6xqfpvy1ycntrp0kesyr0

因数分解 ３乗の公式 文字３つ 高校数学 展開 因数分解 ２１ Youtube

3乗の因数分解の仕方を教えてください 3乗の因数分解の仕方を教えてく 数学 教えて Goo

因数分解のやり方がわからない人必見 公式や解き方のコツをわかりやすく紹介 高校生向け受験応援メディア 受験のミカタ

最も選択された 3 乗 因数 分解 公式

高校数 数と式 因数分解 ３乗 ３乗 の因数分解 オンライン無料塾 ターンナップ Youtube

基本対称式について6乗和の値を因数分解公式を使って求める タロウ岩井のnote Note

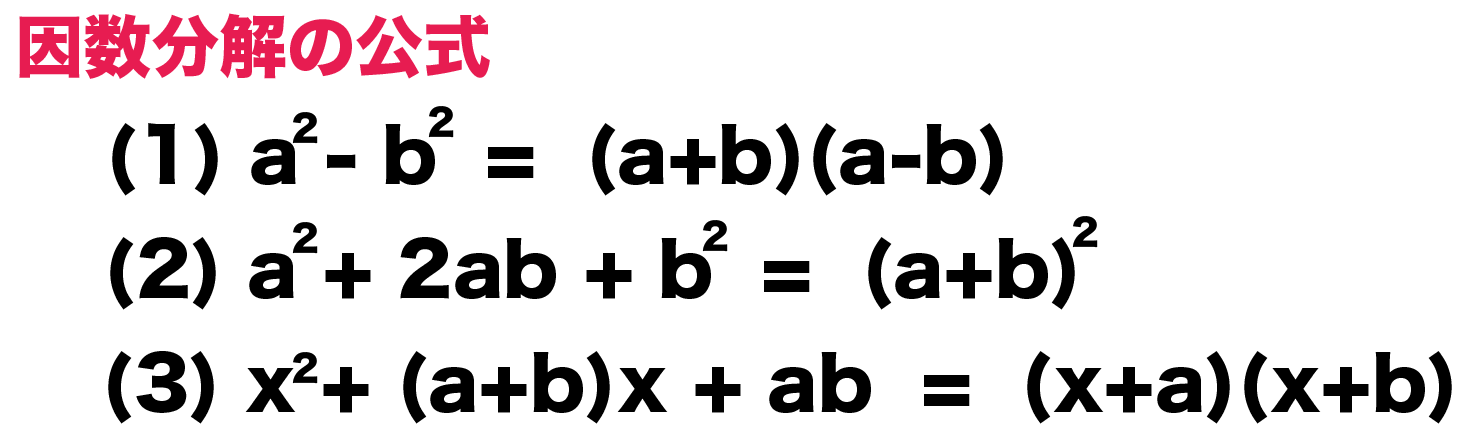
中学数学 因数分解の2つの公式の覚え方 Qikeru 学びを楽しくわかりやすく

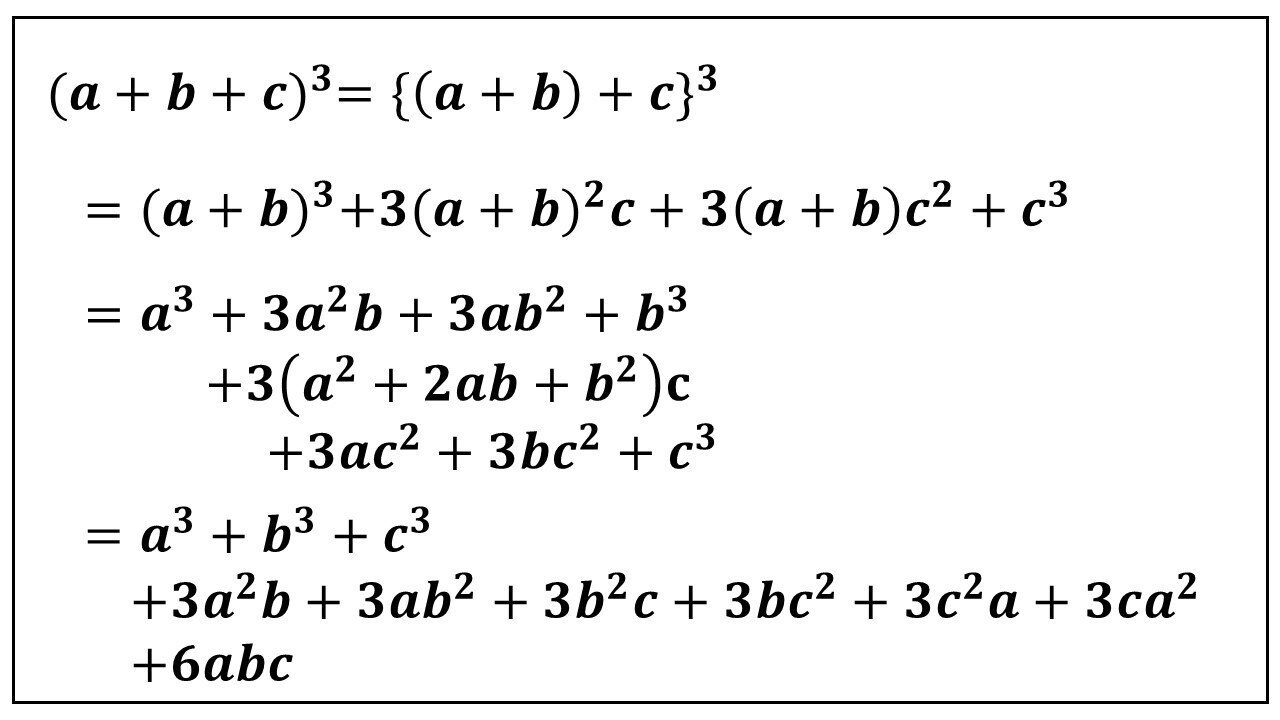
A B Cの2乗や3乗の展開公式 タロウ岩井のnote Note

三乗 3乗の展開 因数分解の公式 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開

数と式 因数分解の公式 3乗の公式 その1 Vol 15 ３回読めば 絶対理解できる看護受験数学 Kazアカデミー 大阪の看護学校 看護予備校

中3数学 因数分解の解き方と対策問題 Examee

X3乗 1 を因数分解するにはどうすればいいですか Clearnote

Studydoctor３乗の因数分解 数 Studydoctor

三乗の展開公式 A B 3乗の計算方法は 問題を使って解説 数スタ

因数分解とは 公式や計算のやり方 問題の解き方 受験辞典

３乗とは 1分でわかる意味 求め方 展開 因数分解 展開公式との関係

3乗の展開 A B A B C 数学i 式の計算 2 Youtube

高校数学 因数分解公式と3次式の因数分解 A B C 3abc 受験の月

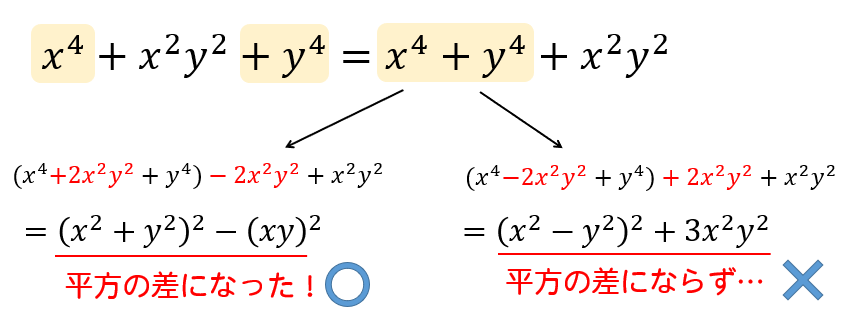
4乗 複二次式の因数分解の解き方 途中式をていねいに解説するぞ 数スタ

因数分解の公式まとめ一覧とその活用例 アタリマエ

3次式の因数分解 公式とやり方について問題を使って解説 数スタ

数学 A B C 二乗の展開公式は 問題の解き方は徹底解説 数スタ

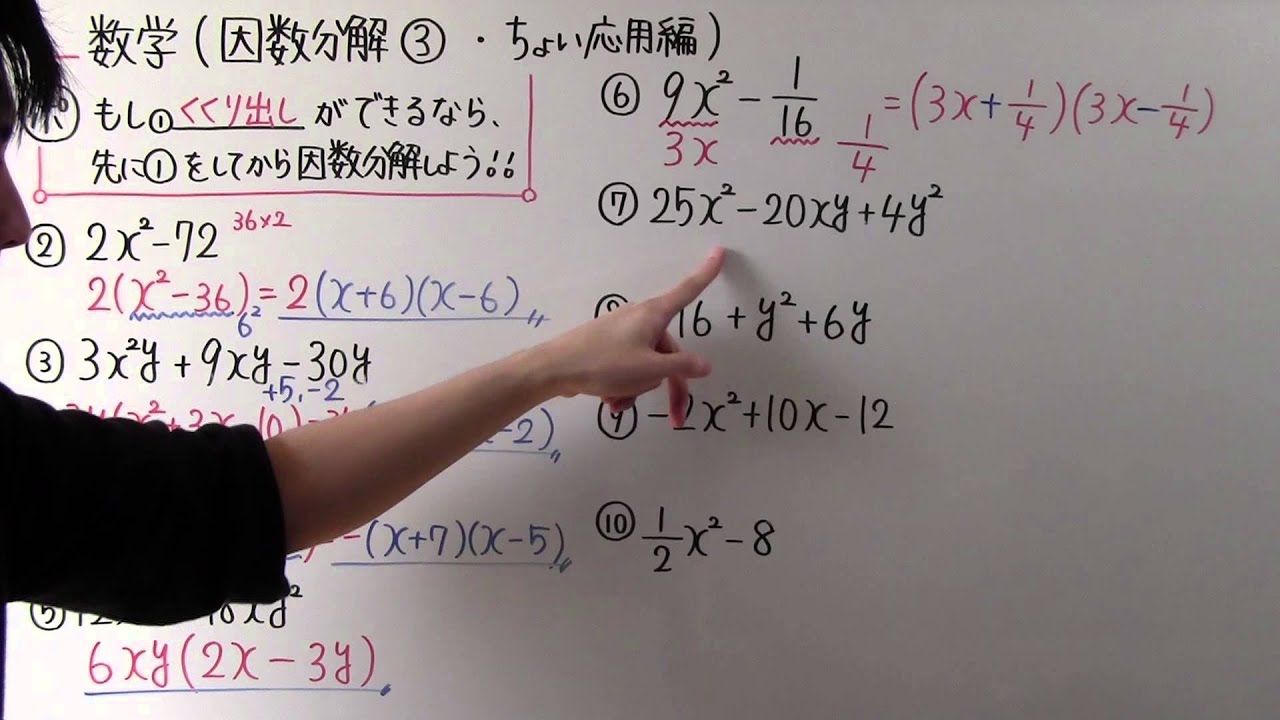
数学 中3 8 因数分解 ちょい応用編 Youtube

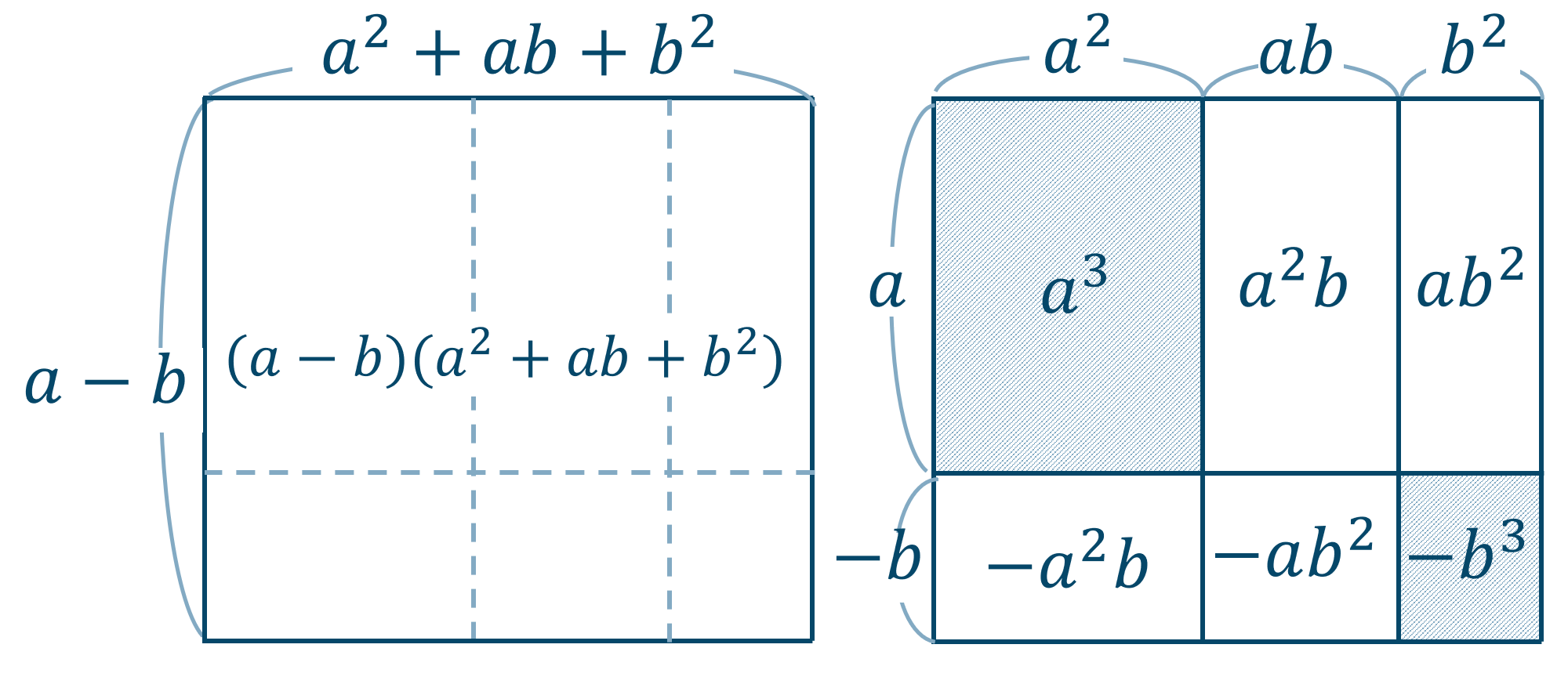
標準 三次式の因数分解と体積 なかけんの数学ノート

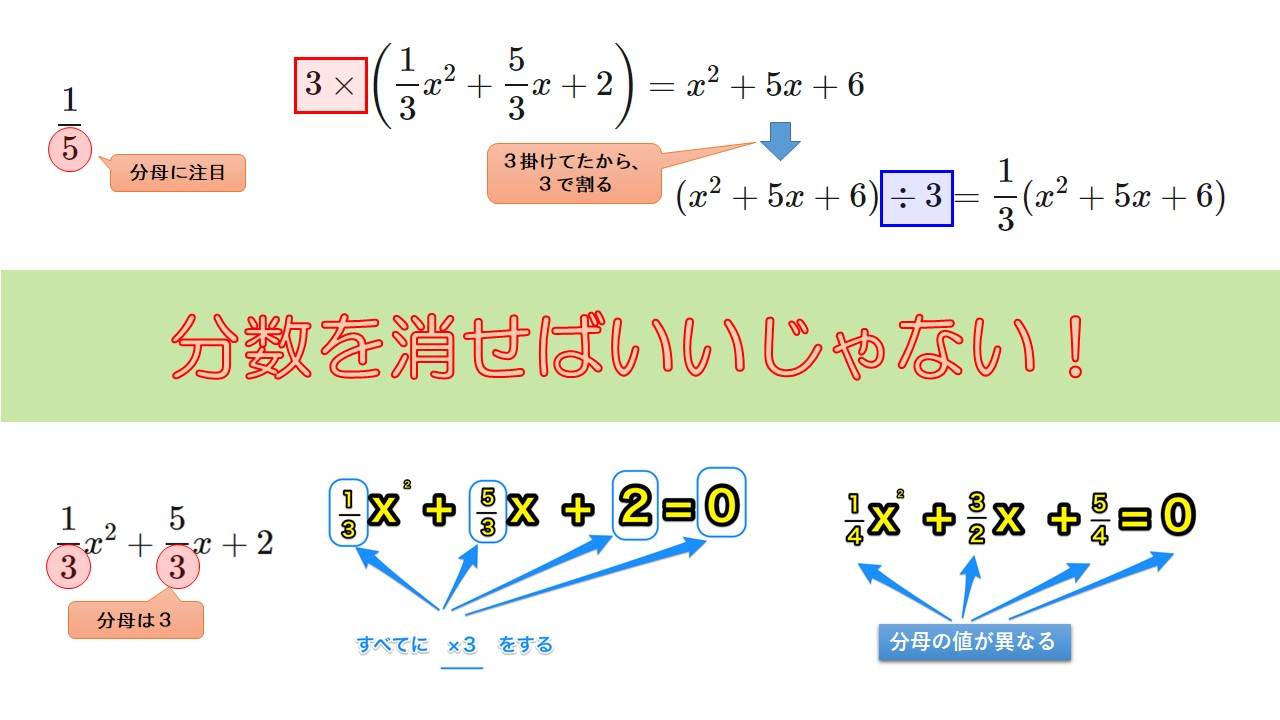
高校数学 因数分解 分数が登場する式を因数分解する方法 わかりやすく解説します 数学の面白いこと 役に立つことをまとめたサイト

三乗の公式 展開と因数分解 高校生向け受験応援メディア 受験のミカタ

式と証明 ３次式の展開について 日々是鍛錬 ひびこれたんれん

因数分解とは 1分でわかる意味 公式の一覧 問題 たすきがけのやり方

高校数学 A 3 B 3の因数分解公式 映像授業のtry It トライイット

３乗の公式 数理研

数の中には 2つ以上の数のかけ算 に変形できるものがたくさんあります 例えば X 2 1 は 素因数分解 分数 教え

三乗根を求める問題です Clearnote

因数分解の問題の解き方とコツ 2乗 3乗公式とたすきがけ アタリマエ

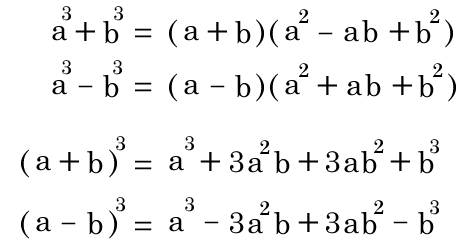
3乗の因数分解 優技録

2の3乗とは 1分でわかる計算 表示方法 2の3乗 2の3乗の計算

3乗根を簡単に暗算で計算できてしまう方法 数学の面白いこと 役に立つことをまとめたサイト

3 Y Online

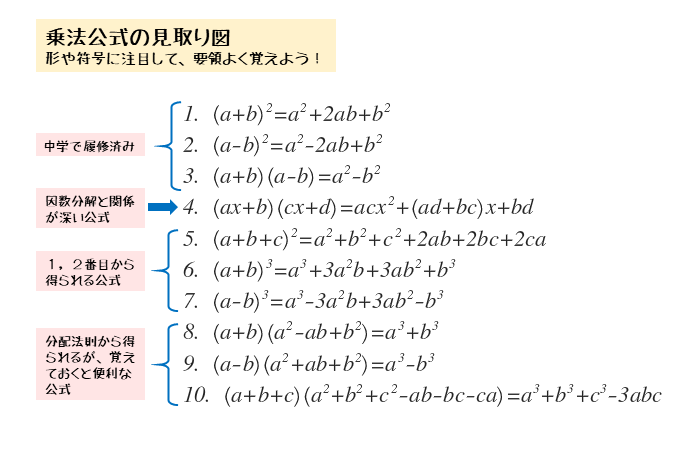
数と式 整式の展開と乗法公式について 日々是鍛錬 ひびこれたんれん

数学 質問解答 ３乗をふくんだ式の因数分解 パート１ 高校数学 数a 因数分解 質問ありがとうございました 行間 ぎょうのあいだ 先生

高校数学 因数分解 3乗が登場する因数分解の解き方をわかりやすく解説 数学の面白いこと 役に立つことをまとめたサイト

数学 質問解答 ３乗をふくんだ式の因数分解 パート２ 高校数学 数a 因数分解 質問ありがとうございました 行間 ぎょうのあいだ 先生

高校数学 因数分解 4乗が登場する式の因数分解 置き換えをして見慣れた形に直して解こう 数学の面白いこと 役に立つことをまとめたサイト

Studydoctor２乗の因数分解 中３数学 Studydoctor

３乗和の公式の証明 怜悧玲瓏 高校数学を天空から俯瞰する

高校数学 数 11 因数分解 ３次式の公式編 Youtube

因数定理を利用した因数分解の練習問題 高校数学の知識庫

数 いろいろな式 ３乗の因数分解 元に に符号逆 教えたい 人のための 数学講座

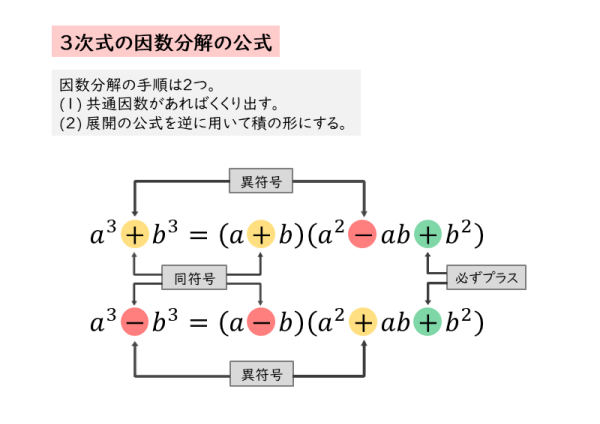
式と証明 ３次式の因数分解について 日々是鍛錬 ひびこれたんれん

高校数学 因数分解 割り算を使った因数分解のやり方を丁寧に説明 数学の面白いこと 役に立つことをまとめたサイト

3乗の因数分解 展開 公式 理系ラボ

展開公式とは 1分でわかる意味 二乗 ３乗の公式 覚え方 問題

因数分解とは 1分でわかる意味 公式の一覧 問題 たすきがけのやり方

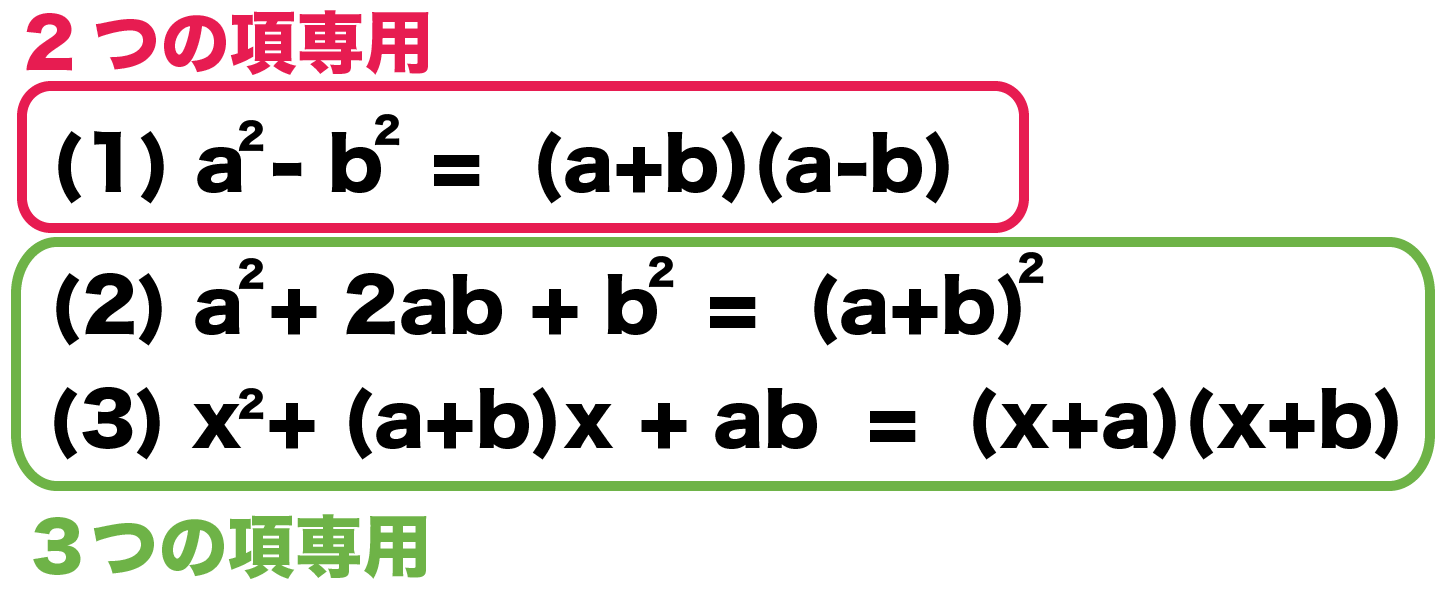
中学数学 因数分解の2つの公式の覚え方 Qikeru 学びを楽しくわかりやすく

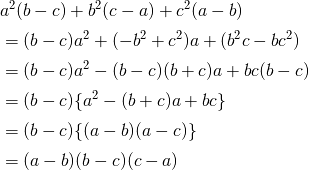
公式いろいろ 因数分解のいろいろな問題とその解き方 スタディクラブ情報局

因数分解できるよね 3乗 東北イタコで学ぶ高校数学 Note

中３ 数学 つまづきやすい因数分解公式の使い方を解説 授業動画あり アオイのホームルーム

2

因数分解の公式の導出方法 3乗公式 4乗公式まで オンライン講師ブログ

乗法公式とは 1分でわかる意味 公式の覚え方 問題 因数分解との関係

三乗の因数分解公式 導出 Youtube

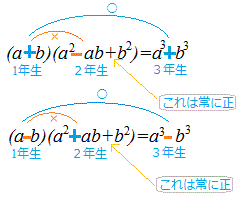
展開公式1

高校数 数と式 因数分解 ３乗の因数分解の整理 オンライン無料塾 ターンナップ Youtube

Incoming Term: 因数分解 公式 3乗,